Introduction to Trigonometry
Trigonometry (from Greek trigōnon, "triangle" and metron, "measure") is a branch of mathematics that studies relationships involving lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies.
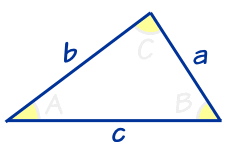
Trigonometry ... is all about triangles.
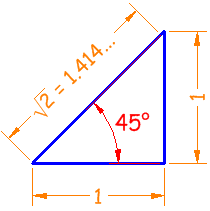
Right Angled Triangle
The triangle of most interest is the right-angled triangle.
We usually know another angle θ.
And we give names to each side:
- Adjacent is adjacent (next to) to the angle θ
- Opposite is opposite the angle θ
- the longest side is the Hypotenuse
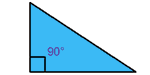 |
A right angled triangle is (you guessed it), a triangle that
has a right angle (90°) in it. |
| The little square in the corner tells us that it is a right angled triangle (I also put 90°, but you don't need to!) |
Two Types
There are two types of right angled triangle:
 | Scalene right angled triangle
One right angle
Two other unequal angles No equal sides |
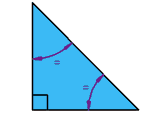 | Isosceles right angled triangle
One right angle
Two other equal angles always of 45° Two equal sides |
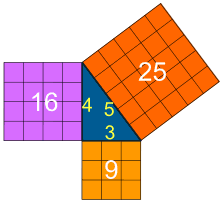
Pythagoras' Theorem

Pythagoras
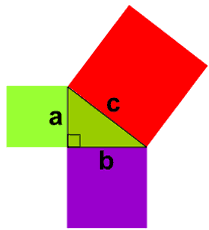
Over 2000 years ago there was an amazing discovery about triangles:
When the triangle has a right angle (90°) ...
... and squares are made on each of the
three sides, then ...
... the biggest square has the exact same area as the other two squares put together!
 It is called "Pythagoras' Theorem" and can be written in one short equation:
a2 + b2 = c2
It is called "Pythagoras' Theorem" and can be written in one short equation:
a2 + b2 = c2
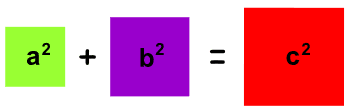 Note:
Note:
- c is the longest side of the triangle
- a and b are the other two sides
 Pythagoras
Over 2000 years ago there was an amazing discovery about triangles:
When the triangle has a right angle (90°) ...
... and squares are made on each of the
three sides, then ... | |
| ... the biggest square has the exact same area as the other two squares put together! | |

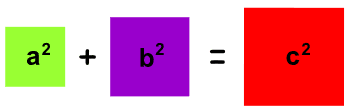
Definition
The longest side of the triangle is called the "hypotenuse", so the formal definition is:
In a right angled triangle:
the square of the hypotenuse is equal to
the sum of the squares of the other two sides.
In a right angled triangle:
the square of the hypotenuse is equal to
the sum of the squares of the other two sides.
the square of the hypotenuse is equal to
the sum of the squares of the other two sides.
Sure ... ?
Let's see if it really works using an example.
Example: A "3,4,5" triangle has a right angle in it.
Why Is This Useful?
If we know the lengths of two sides of a right angled triangle, we can find the length of the third side. (But remember it only works on right angled triangles!)
How Do I Use it?
Write it down as an equation:
a2 + b2 = c2
 | a2 + b2 = c2 |
Example: Solve this triangle.
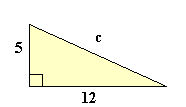
a2 + b2 = c2
52 + 122 = c2
25 + 144 = c2
169 = c2
c2 = 169
c = √169
c = 13
 |
a2 + b2 = c2
52 + 122 = c2
25 + 144 = c2
169 = c2
c2 = 169
c = √169
c = 13
|
"Sine, Cosine and Tangent"
Trigonometry is good at find a missing side or angle in a triangle.
The special functions Sine, Cosine and Tangent help us!
They are simply one side of a triangle divided by another.
For any angle "θ":

Sine Function:
| sin(θ) = Opposite / Hypotenuse |
Cosine Function:
| cos(θ) = Adjacent / Hypotenuse |
Tangent Function:
| tan(θ) = Opposite / Adjacent |
(Sine, Cosine and Tangent are often abbreviated to sin, cos and tan.)
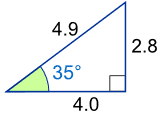
Example: What is the sine of 35°?
Calculators have sin, cos and tan, let's see how to use them:
Example: What is the missing length here?
Sine, Cosine and Tangent
Three Functions, but same idea.
Three Functions, but same idea.
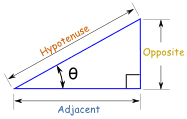
Right Triangle
Sine, Cosine and Tangent are all based on a Right-Angled Triangle
Before getting stuck into the functions, it helps to give a name to each side of a right triangle:
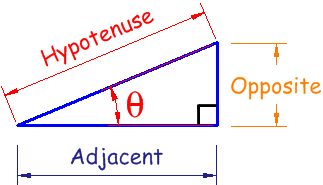
- "Opposite" is opposite to the angle θ
- "Adjacent" is adjacent (next to) to the angle θ
- "Hypotenuse" is the long one
 Adjacent is always next to the angle
And Opposite is opposite the angle
Adjacent is always next to the angle
And Opposite is opposite the angle
Sine, Cosine and Tangent are all based on a Right-Angled Triangle
Before getting stuck into the functions, it helps to give a name to each side of a right triangle:

- "Opposite" is opposite to the angle θ
- "Adjacent" is adjacent (next to) to the angle θ
- "Hypotenuse" is the long one

Adjacent is always next to the angle
And Opposite is opposite the angle
|
Sine, Cosine and Tangent
Sine, Cosine and Tangent are the three main functions in trigonometry.
They are often shortened to sin, cos and tan.
To calculate them:
Divide the length of one side by another side
... but which sides?
For a triangle with an angle θ, they are calculated this way:
Sine Function:
sin(θ) = Opposite / Hypotenuse
Cosine Function:
cos(θ) = Adjacent / Hypotenuse
Tangent Function:
tan(θ) = Opposite / Adjacent
In picture form:

Sine, Cosine and Tangent are the three main functions in trigonometry.
They are often shortened to sin, cos and tan.
To calculate them:
Divide the length of one side by another side
... but which sides?
... but which sides?
For a triangle with an angle θ, they are calculated this way:
Sine Function:
| sin(θ) = Opposite / Hypotenuse |
Cosine Function:
| cos(θ) = Adjacent / Hypotenuse |
Tangent Function:
| tan(θ) = Opposite / Adjacent |
In picture form:

Example: What is the sine of 35°?
How to remember? Think "Sohcahtoa"! It works like this:
Soh...
Sine = Opposite / Hypotenuse
...cah...
Cosine = Adjacent / Hypotenuse
...toa
Tangent = Opposite / Adjacent
You can read more about sohcahtoa ... please remember it, it may help in an exam !
How to remember? Think "Sohcahtoa"! It works like this:
Soh...
|
Sine = Opposite / Hypotenuse
|
...cah...
|
Cosine = Adjacent / Hypotenuse
|
...toa
|
Tangent = Opposite / Adjacent
|
You can read more about sohcahtoa ... please remember it, it may help in an exam !
Examples
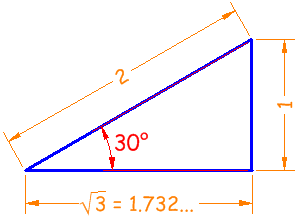
Example: what are the sine, cosine and tangent of 30° ?
Example: what are the sine, cosine and tangent of 45° ?
Why?
Why are these functions important?
- Because they let us work out angles when we know sides
- And they let us work out sides when we know angles
Why are these functions important?
- Because they let us work out angles when we know sides
- And they let us work out sides when we know angles
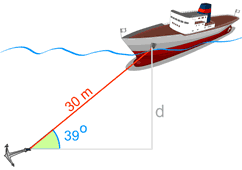
Example: Use the sine function to find "d"
Degrees and Radians
Angles can be in Degrees or Radians. Here are some examples:
Angle Degrees Radians  Right Angle
Right Angle 90° π/2 __ Straight Angle 180° π  Full Rotation
Full Rotation360° 2π
| Angle | Degrees | Radians |
|---|---|---|
| 90° | π/2 | |
| __ Straight Angle | 180° | π |
| 360° | 2π |
Degrees (Angles)
We can measure Angles in Degrees.
There are 360 degrees in one Full Rotation (one
complete circle around).
(Angles can also be measured in Radians)
|
(Note: "Degrees" can also mean Temperature, but here we are talking about Angles)
The Degree Symbol: °
We use a little circle ° following the number to mean degrees.
For example 90° means 90 degrees
One Degree

This is how large 1 Degree is
This is how large 1 Degree is
The Full Circle
A Full Circle is 360°
Half a circle is 180°
(called a Straight Angle)
Quarter of a circle is 90°
(called a Right Angle)

Why 360 degrees? Probably because old calendars (such as the Persian Calendar) used 360 days for a year - when they watched the stars they saw them revolve around the North Star one degree per day.
Also 360 can be divided evenly by 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 and 180, which makes a lot of basic geometry easier.
A Full Circle is 360°
Half a circle is 180°
(called a Straight Angle)
Quarter of a circle is 90°
(called a Right Angle) |  |
Why 360 degrees? Probably because old calendars (such as the Persian Calendar) used 360 days for a year - when they watched the stars they saw them revolve around the North Star one degree per day.
Also 360 can be divided evenly by 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 and 180, which makes a lot of basic geometry easier.
|
Measuring Degrees
We often measure degrees using a protractor:
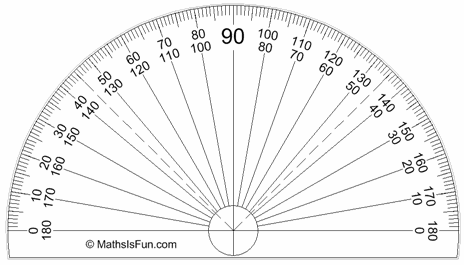
The normal protractor measures 0° to 180°

The normal protractor measures 0° to 180°
 |
There are also full-circle protractors.
But they are not as commonly used because they are a bit big and don't do anything special.
|
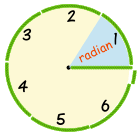
Radians
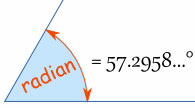 |
We can measure Angles in Radians.
1 Radian is about 57.2958 degrees.
|
Does 57.2958... degrees seem a strange value?
Maybe degrees are strange, as the Radian is a pure measure based on the Radius of the circle:
Maybe degrees are strange, as the Radian is a pure measure based on the Radius of the circle:
Radian: the angle made by taking the radius
and wrapping it along the edge of a circle:
and wrapping it along the edge of a circle:
| So, a Radian "cuts out" a length of a circle's circumference equal to the radius. | 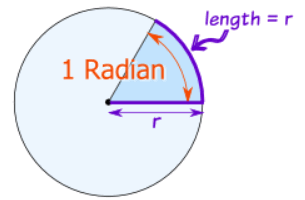 |
Radians and Degrees
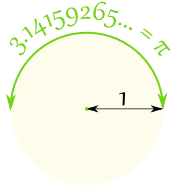 So:
So:
- There are π radians in a half circle
- And also 180° in a half circle
So π radians = 180°
So 1 radian = 180°/π = 57.2958° (approximately)
Degrees Radians
(exact) Radians
(approx) 30° π/6 0.524 45° π/4 0.785 60° π/3 1.047 90° π/2 1.571 180° π 3.142 270° 3π/2 4.712 360° 2π 6.283

| Degrees | Radians (exact) | Radians (approx) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0.785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1.571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4.712 |
| 360° | 2π | 6.283 |
Example: How Many Radians in a Full Circle?
Radians Preferred by Mathematicians
Because the radian is based on the pure idea of "the radius being laid along the circumference", it often gives simple and natural results when used in mathematics.
For example, look at the sine function for very small values:
x (radians) 1 0.1 0.01 0.001 sin(x) 0.8414710 0.0998334 0.0099998 0.0009999998
For very small values. "x" and "sin(x)" are almost the same
(as long as "x" is in Radians!)
There will be other examples like that as you learn more about mathematics.
| x (radians) | 1 | 0.1 | 0.01 | 0.001 |
|---|---|---|---|---|
| sin(x) | 0.8414710 | 0.0998334 | 0.0099998 | 0.0009999998 |
(as long as "x" is in Radians!)
Conclusion
So, degrees are easier to use in everyday work, but radians are much better for mathematics.
Other Functions (Cotangent, Secant, Cosecant)
Similar to Sine, Cosine and Tangent, there are three other trigonometric functions which are made by dividing one side by another:

Cosecant Function:
csc(θ) = Hypotenuse / Opposite
Secant Function:
sec(θ) = Hypotenuse / Adjacent
Cotangent Function:
cot(θ) = Adjacent / Opposite
Similar to Sine, Cosine and Tangent, there are three other trigonometric functions which are made by dividing one side by another:

Cosecant Function:
| csc(θ) = Hypotenuse / Opposite |
Secant Function:
| sec(θ) = Hypotenuse / Adjacent |
Cotangent Function:
| cot(θ) = Adjacent / Opposite |
Trigonometric and Triangle Identities
And as you get better at Trigonometry you can learn these:

The Trigonometric Identities are equations that are true for all right-angled triangles.
The Triangle Identities are equations that are true for all triangles (they don't have to have a right angle).
And as you get better at Trigonometry you can learn these:
 |
The Trigonometric Identities are equations that are true for all right-angled triangles.
|
 |
The Triangle Identities are equations that are true for all triangles (they don't have to have a right angle).
|
Trigonometric Identities
Right Triangle
The Trigonometric Identities are equations that are true for Right Angled Triangles. (If it is not a Right Angled Triangle go to the Triangle Identities page.)
Each side of a right triangle has a name:

 Adjacent is always next to the angle
And Opposite is opposite the angle
Adjacent is always next to the angle
And Opposite is opposite the angle
We are soon going to be playing with all sorts of functions, but remember it all comes back to that simple triangle with:
- Angle θ
- Hypotenuse
- Adjacent
- Opposite
The Trigonometric Identities are equations that are true for Right Angled Triangles. (If it is not a Right Angled Triangle go to the Triangle Identities page.)
Each side of a right triangle has a name:


Adjacent is always next to the angle
And Opposite is opposite the angle
|
We are soon going to be playing with all sorts of functions, but remember it all comes back to that simple triangle with:
- Angle θ
- Hypotenuse
- Adjacent
- Opposite
Sine, Cosine and Tangent
The three main functions in trigonometry are Sine, Cosine and Tangent.
They are just the length of one side divided by another
For a right triangle with an angle θ :

Sine Function:
sin(θ) = Opposite / Hypotenuse
Cosine Function:
cos(θ) = Adjacent / Hypotenuse
Tangent Function:
tan(θ) = Opposite / Adjacent
Also, when we divide Sine by Cosine we get:
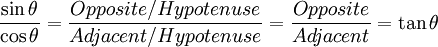 So we can say:
tan(θ) = sin(θ)/cos(θ)
That is our first Trigonometric Identity.
So we can say:
tan(θ) = sin(θ)/cos(θ)
That is our first Trigonometric Identity.
The three main functions in trigonometry are Sine, Cosine and Tangent.
They are just the length of one side divided by another
For a right triangle with an angle θ :

Sine Function:
| sin(θ) = Opposite / Hypotenuse |
Cosine Function:
| cos(θ) = Adjacent / Hypotenuse |
Tangent Function:
| tan(θ) = Opposite / Adjacent |
Also, when we divide Sine by Cosine we get:
So we can say:
tan(θ) = sin(θ)/cos(θ)
That is our first Trigonometric Identity.
Cosecant, Secant and Cotangent
We can also divide "the other way around" (such as Adjacent/Opposite instead ofOpposite/Adjacent):

Cosecant Function:
csc(θ) = Hypotenuse / Opposite
Secant Function:
sec(θ) = Hypotenuse / Adjacent
Cotangent Function:
cot(θ) = Adjacent / Opposite
We can also divide "the other way around" (such as Adjacent/Opposite instead ofOpposite/Adjacent):

Cosecant Function:
| csc(θ) = Hypotenuse / Opposite |
Secant Function:
| sec(θ) = Hypotenuse / Adjacent |
Cotangent Function:
| cot(θ) = Adjacent / Opposite |
Example: when Opposite = 2 and Hypotenuse = 4 then
Because of all that we can say:
sin(θ) = 1/csc(θ)
cos(θ) = 1/sec(θ)
tan(θ) = 1/cot(θ)
And the other way around:
csc(θ) = 1/sin(θ)
sec(θ) = 1/cos(θ)
cot(θ) = 1/tan(θ)
And we also have:
cot(θ) = cos(θ)/sin(θ)
Because of all that we can say:
sin(θ) = 1/csc(θ)
cos(θ) = 1/sec(θ)
tan(θ) = 1/cot(θ)
And the other way around:
csc(θ) = 1/sin(θ)
sec(θ) = 1/cos(θ)
cot(θ) = 1/tan(θ)
And we also have:
cot(θ) = cos(θ)/sin(θ)
Pythagoras Theorem
For the next trigonometric identities we start with Pythagoras' Theorem:

The Pythagorean Theorem says that, in a right triangle, the square of a plus the square of b is equal to the square of c:
a2 + b2 = c2
Dividing through by c2 gives
a2 + b2 = c2 c2 c2 c2
This can be simplified to:
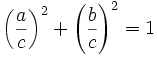 Now, a/c is Opposite / Hypotenuse, which is sin(θ)
And b/c is Adjacent / Hypotenuse, which is cos(θ)
So (a/c)2 + (b/c)2 = 1 can also be written:
sin2 θ + cos2 θ = 1
Now, a/c is Opposite / Hypotenuse, which is sin(θ)
And b/c is Adjacent / Hypotenuse, which is cos(θ)
So (a/c)2 + (b/c)2 = 1 can also be written:
sin2 θ + cos2 θ = 1
For the next trigonometric identities we start with Pythagoras' Theorem:
 |
The Pythagorean Theorem says that, in a right triangle, the square of a plus the square of b is equal to the square of c:
a2 + b2 = c2
|
Dividing through by c2 gives
| a2 | + | b2 | = | c2 |
| c2 | c2 | c2 |
This can be simplified to:
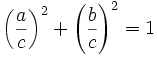
Now, a/c is Opposite / Hypotenuse, which is sin(θ)
And b/c is Adjacent / Hypotenuse, which is cos(θ)
So (a/c)2 + (b/c)2 = 1 can also be written:
sin2 θ + cos2 θ = 1
Example: 32°
Related identities include:
sin2 θ = 1 − cos2 θ
cos2 θ = 1 − sin2 θ
tan2 θ + 1 = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
Related identities include:
sin2 θ = 1 − cos2 θ
cos2 θ = 1 − sin2 θ
tan2 θ + 1 = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
cos2 θ = 1 − sin2 θ
tan2 θ + 1 = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
How Do You Remember Them?
But Wait ... There is More!
There are many more identities ... here are some of the more useful ones:
There are many more identities ... here are some of the more useful ones:
Opposite Angle Identities
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
Double Angle Identities
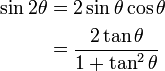 |
 |
Half Angle Identities
Note that "±" means it may be either one, depending on the value of θ/2
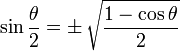
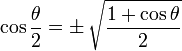
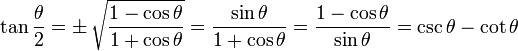
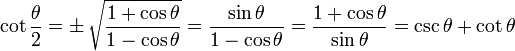
Note that "±" means it may be either one, depending on the value of θ/2
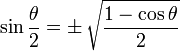 |
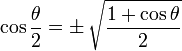 |
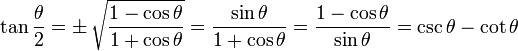 |
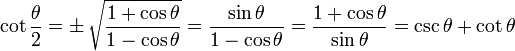 |
Angle Sum and Difference Identities
Note that  means you can use plus or minus, and the
means you can use plus or minus, and the  means to use the opposite sign.
means to use the opposite sign.
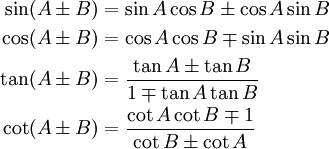
Note that  means you can use plus or minus, and the
means you can use plus or minus, and the  means to use the opposite sign.
means to use the opposite sign.
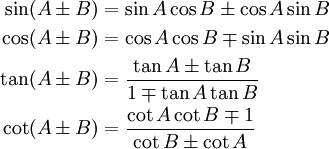
Triangle Identities
There are also Triangle Identities which apply to all triangles (not just Right Angled Triangles)
There are also Triangle Identities which apply to all triangles (not just Right Angled Triangles)
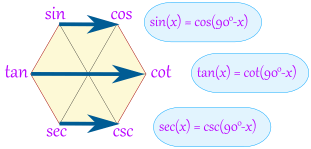
Magic Hexagon for Trig Identities
This hexagon is a special diagram
to help you remember some Trigonometric Identities 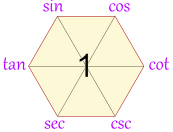
Sketch the diagram when you are struggling with trig identities ... it may help you! Here is how:
| This hexagon is a special diagram to help you remember some Trigonometric Identities |  |
Sketch the diagram when you are struggling with trig identities ... it may help you! Here is how:
Building It: The Quotient Identities
Start with:
tan(x) = sin(x) / cos(x)
To help you remember
think "tsc !"
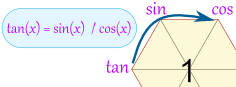
Then add:
- cot (which is cotangent) on the opposite
side of the hexagon to tan
- csc (which is cosecant) next, and
- sec (which is secant) last

To help you remember: the "co" functions are all on the right
OK, we have now built our hexagon, what do we get out of it?
Well, we can now follow "around the clock" (either direction) to get all the "Quotient Identities":
Clockwise
- tan(x) = sin(x) / cos(x)
- sin(x) = cos(x) / cot(x)
- cos(x) = cot(x) / csc(x)
- cot(x) = csc(x) / sec(x)
- csc(x) = sec(x) / tan(x)
- sec(x) = tan(x) / sin(x)
Counterclockwise
- cos(x) = sin(x) / tan(x)
- sin(x) = tan(x) / sec(x)
- tan(x) = sec(x) / csc(x)
- sec(x) = csc(x) / cot(x)
- csc(x) = cot(x) / cos(x)
- cot(x) = cos(x) / sin(x)
Start with:
tan(x) = sin(x) / cos(x)
| 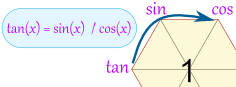 | ||
Then add:
|  | ||
| To help you remember: the "co" functions are all on the right | |||
OK, we have now built our hexagon, what do we get out of it?
Well, we can now follow "around the clock" (either direction) to get all the "Quotient Identities":
| Clockwise |
|
| Counterclockwise |
|
Product Identities
The hexagon also shows that a function between any two functions is equal to them multiplied together (if they are opposite each other, then the "1" is between them):
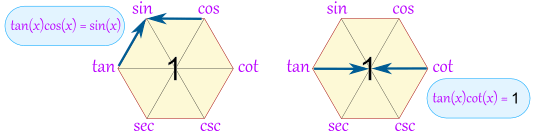
Example: tan(x)cos(x) = sin(x) Example: tan(x)cot(x) = 1
Some more examples:
- sin(x)csc(x) = 1
- tan(x)csc(x) = sec(x)
- sin(x)sec(x) = tan(x)
The hexagon also shows that a function between any two functions is equal to them multiplied together (if they are opposite each other, then the "1" is between them):
 | |
| Example: tan(x)cos(x) = sin(x) | Example: tan(x)cot(x) = 1 |
Some more examples:
- sin(x)csc(x) = 1
- tan(x)csc(x) = sec(x)
- sin(x)sec(x) = tan(x)
But Wait, There is More!
You can also get the "Reciprocal Identities", by going "through the 1"
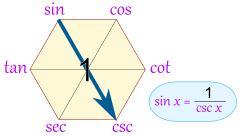
Here you can see that sin(x) = 1 / csc(x)
Here is the full set:
- sin(x) = 1 / csc(x)
- cos(x) = 1 / sec(x)
- cot(x) = 1 / tan(x)
- csc(x) = 1 / sin(x)
- sec(x) = 1 / cos(x)
- tan(x) = 1 / cot(x)
You can also get the "Reciprocal Identities", by going "through the 1"
 | Here you can see that sin(x) = 1 / csc(x) |
Here is the full set:
- sin(x) = 1 / csc(x)
- cos(x) = 1 / sec(x)
- cot(x) = 1 / tan(x)
- csc(x) = 1 / sin(x)
- sec(x) = 1 / cos(x)
- tan(x) = 1 / cot(x)
Bonus!
AND we also get these:
 Examples:
Examples:
- sin(30°) = cos(60°)
- tan(80°) = cot(10°)
- sec(40°) = csc(50°)
AND we also get these:

Examples:
- sin(30°) = cos(60°)
- tan(80°) = cot(10°)
- sec(40°) = csc(50°)
Double Bonus: The Pythagorean Identities
The Unit Circle shows us that
sin2 x + cos2 x = 1
The magic hexagon can help us remember that, too, by going clockwise around any of these three triangles:
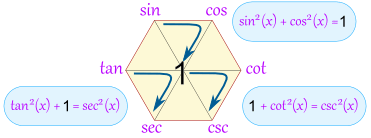 And we have:
And we have:
- sin2(x) + cos2(x) = 1
- 1 + cot2(x) = csc2(x)
- tan2(x) + 1 = sec2(x)
You can also travel counterclockwise around a triangle, for example:
- 1 - cos2(x) = sin2(x)
The Unit Circle shows us that
sin2 x + cos2 x = 1
The magic hexagon can help us remember that, too, by going clockwise around any of these three triangles:

And we have:
- sin2(x) + cos2(x) = 1
- 1 + cot2(x) = csc2(x)
- tan2(x) + 1 = sec2(x)
You can also travel counterclockwise around a triangle, for example:
- 1 - cos2(x) = sin2(x)
Hope this helps you!
Triangle Identities
Triangle Identities
The triangle identities are equations that are true for all triangles (they don't need to have a right angle). For the identities involving right angles triangles see Trigonometric Identities.
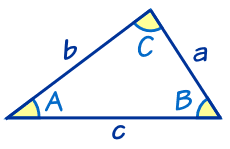
The triangle identities are equations that are true for all triangles (they don't need to have a right angle). For the identities involving right angles triangles see Trigonometric Identities.

Law of Sines
The Law of Sines (also known as The Sine Rule) is:
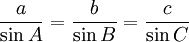 it can also be this way around:
it can also be this way around:
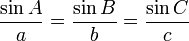
The Law of Sines (also known as The Sine Rule) is:
it can also be this way around:
Law of Cosines
The Law of Cosines (also known as The Cosine Rule) is an extension of the Pythagorean Theorem to any triangle:
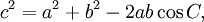 which can also be re-arranged to:
which can also be re-arranged to:

The Law of Cosines (also known as The Cosine Rule) is an extension of the Pythagorean Theorem to any triangle:
which can also be re-arranged to:
Law of Tangents
The Law of Tangents is:
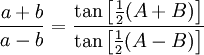
The Law of Tangents is:
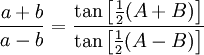


No comments:
Post a Comment