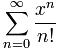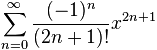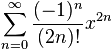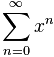Taylor Series

A Taylor Series is an expansion of a function into an infinite sum of terms, like these ones:

Taylor Series expansion	As Sigma Notation

(There are many more)

Approximations

You can use the first few terms of a Taylor Series to get an approximate value for a function.

Here we show better and better approximations for cos(x). The red line is cos(x), the blue is the approximation (try plotting it yourself) :

1 − x2/2!
1 − x2/2! + x4/4!
1 − x2/2! + x4/4! − x6/6!
1 − x2/2! + x4/4! − x6/6! + x8/8!

(You can also see the Taylor Series in action at Euler's Formula for Complex Numbers.)

What is this Magic?

How can you turn a function into a series of power terms like this?

Well, it isn't really magic. First you say you want to have this:

f(x) = c₀ + c₁(x-a) + c₂(x-a)² + c₃(x-a)³ + ...

Then choose a value "a", and work out the values c₀ , c₁ , c₂ , ... etc

It is done using derivatives ...

Quick review: a derivative gives you the slope of a function at any point.

You must know the derivatives of your function f(x) and these basic derivative rules :

• The derivative of a constant is 0
• The derivative of x is 1
• The derivative of xⁿ is nx^n-1 (Example: the derivative of x³ is 3x²)

We will use the little mark ’ to mean "derivative of".

OK, let's start:

To get c₀, choose x=a so all the (x-a) terms become zero, leaving you with:

f(a) = c₀

So c₀ = f(a)

To get c₁, take the derivative of f(x):

f’(x) = c₁ + 2c₂(x-a) + 3c₃(x-a)² + ...

With x=a all the (x-a) terms become zero:

f’(a) = c₁

So c₁ = f’(a)

To get c₂, do the derivative again:

f’’(x) = 2c₂ + 3×2×c₃(x-a) + ...

With x=a all the (x-a) terms become zero:

f’’(a) = 2c₂

So c₂ = f’’(a)/2

In fact, a pattern is emerging. Each term is

• the next higher derivative ...
• ... divided by all the exponents so far multiplied together (for which we can use factorial notation, for example 3! = 3×2×1)

And we get:

Now we have a way of finding our own Taylor Series: keep taking derivatives and divide by n! each time.

Example: Taylor Series for cos(x)

And all we need to know is:

• The derivative of cos(x) is -sin(x)
• The derivative of sin(x) is cos(x)

Choose a=0:

• c₀ = f(0) = cos(0) = 1
• c₁ = f'(0)/1! = -sin(0) = 0
• c₂ = f''(0)/2! = -cos(0)/2! = -1/2!
• c₃ = f'''(0)/3! = sin(0)/3! = 0
• c₄ = f''''(0)/4! = cos(0)/4! = 1/4!
• etc...

The odd terms are all zero, so we get:

cos(x) = 1 − x²/2! + x⁴/4! − ...

Try that for sin(x) yourself, it will help you to learn.

Or try it on another function of your choosing. The key thing is that you be able to take derivatives of your function f(x).

Note: A Maclaurin Series is a Taylor Series where a=0, so all the examples we have been using so far can also be called Maclaurin Series.

Derivative Rules

The Derivative tells us the slope of a function at any point.

The derivatives of many functions are well known. Here are some useful rules to help you work out the derivatives of more complicated functions (with examples below). Note: the little mark ’means "Derivative of".

Common Functions	Function	Derivative
Constant	c	0
	x	1
Square	x2	2x
Square Root	√x	(½)x-½
Exponential	ex	ex
	ax	ax(ln a)
Logarithms	ln(x)	1/x
	loga(x)	1 / (x ln(a))
Trigonometry (x is in radians)	sin(x)	cos(x)
	cos(x)	−sin(x)
	tan(x)	sec2(x)
	sin-1(x)	1/√(1−x2)
	cos-1(x)	−1/√(1−x2)
	tan-1(x)	1/(1+x2)
Rules	Function	Derivative
Multiplication by constant	cf	cf’
Power Rule	xn	nxn−1
Sum Rule	f + g	f’ + g’
Difference Rule	f - g	f’ − g’
Product Rule	fg	f g’ + f’ g
Quotient Rule	f/g	(f’ g − g’ f )/g2
Reciprocal Rule	1/f	−f’/f2
Chain Rule (as "Composition of Functions")	f º g	(f’ º g) × g’
Chain Rule (in a different form)	f(g(x))	f’(g(x))g’(x)

"The derivative of" is also written 

Examples

Example: what is the derivative of sin(x) ?

From the table above it is listed as being cos(x)

It can be written as:

sin(x) = cos(x)

Or:

sin(x)’ = cos(x)

Power Rule

Example: What is x³ ?

The question is asking "what is the derivative of x³?"

We can use the Power Rule, where n=3:

xⁿ = nxⁿ⁻¹

x³ = 3x³⁻¹ = 3x²

Example: What is (1/x) ?

1/x is also x^-1

We can use the Power Rule, where n = −1:

xⁿ = nxⁿ⁻¹

x⁻¹ = −1x⁻¹⁻¹ = −x⁻²

Multiplication by constant

Example: What is 5x³ ?

the derivative of cf = cf’

the derivative of 5f = 5f’

We know (from the Power Rule):

x³ = 3x³⁻¹ = 3x²

So:

5x³ = 5x³ = 5 × 3x² = 15x²

Sum Rule

Example: What is the derivative of x²+x³ ?

The Sum Rule says:

the derivative of f + g = f’ + g’

So we can work out each derivative separately and then add them.

Using the Power Rule:

• x² = 2x
• x³ = 3x²

And so:

the derivative of x² + x³ = 2x + 3x²

Difference Rule

It doesn't have to be x, we can differentiate with respect to, for example, v:

Example: What is (v³−v⁴) ?

The Difference Rule says

the derivative of f − g = f’ − g’

So we can work out each derivative separately and then subtract them.

Using the Power Rule:

• v³ = 3v²
• v⁴ = 4v³

And so:

the derivative of v³ − v⁴ = 3v² − 4v³

Sum, Difference, Constant Multiplication And Power Rules

Example: What is (5z² + z³ − 7z⁴) ?

Using the Power Rule:

• z² = 2z
• z³ = 3z²
• z⁴ = 4z³

And so:

(5z² + z³ − 7z⁴) = 5 × 2z + 3z² − 7 × 4z³ = 10z + 3z² − 28z³

Product Rule

Example: What is the derivative of cos(x)sin(x) ?

The Product Rule says:

the derivative of fg = f g’ + f’ g

In our case:

• f = cos
• g = sin

We know (from the table above):

• cos(x) = −sin(x)
• sin(x) = cos(x)

So:

the derivative of cos(x)sin(x) = cos(x)cos(x) − sin(x)sin(x)

= cos²(x) − sin²(x)

 

Reciprocal Rule

Example: What is (1/x) ?

The Reciprocal Rule says:

the derivative of 1/f = −f’/f²

With f(x)= x, we know that f’(x) = 1

So:

the derivative of 1/x = −1/x²

Which is the same result we got above using the Power Rule.

Chain Rule

Example: What is sin(x²) ?

sin(x²) is made up of sin() and x²:

• f(g) = sin(g)
• g(x) = x²

The Chain Rule says:

the derivative of f(g(x)) = f'(g(x))g'(x)

The individual derivatives are:

• f'(g) = cos(g)
• g'(x) = 2x

So:

sin(x²) = cos(g(x)) × 2x

= 2x cos(x²)

Example: What is (1/sin(x)) ?

1/sin(x) is made up of 1/g and sin():

• f(g) = 1/g
• g(x) = sin(x)

The Chain Rule says:

the derivative of f(g(x)) = f’(g(x))g’(x)

The individual derivatives are:

• f'(g) = −1/(g²)
• g'(x) = cos(x)

So:

(1/sin(x))’ = −1/(g(x))² × cos(x)

= −cos(x)/sin²(x)

Example: What is (5x−2)³ ?

The Chain Rule says:

the derivative of f(g(x)) = f’(g(x))g’(x)

(5x-2)³ is made up of g³ and 5x-2:

• f(g) = g³
• g(x) = 5x−2

The individual derivatives are:

• f'(g) = 3g² (by the Power Rule)
• g'(x) = 5

So:

(5x−2)³ = 3g(x)² × 5 = 15(5x−2)²

Functions

What is a Function?

A function relates an input to an output.

It is like a machine that has an input and an output. And the output is related somehow to the input.

f(x)	"f(x) = ... " is the classic way of writing a function. And there are other ways, as you will see!

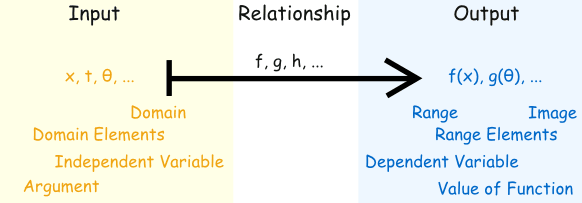
Input, Relationship, Output

We will see many ways to think about functions, but there are always three main parts:

• The input
• The relationship
• The output

Example: "Multiply by 2" is a very simple function.

Here are the three parts:

Input	Relationship	Output
0	× 2	0
1	× 2	2
7	× 2	14
10	× 2	20
...	...	...

For an input of 50, what is the output?

Some Examples of Functions

x² (squaring) is a function
x³+1 is also a function
Sine, Cosine and Tangent are functions used in trigonometry
and there are lots more!

But we are not going to look at specific functions ...
... instead we will look at the general idea of a function.

Names

First, it is useful to give a function a name.

The most common name is "f", but we can have other names like "g" ... or even "marmalade" if we want.

But let's use "f":

We say "f of x equals x squared"

what goes into the function is put inside parentheses () after the name of the function:

So f(x) shows us the function is called "f", and "x" goes in

And we usually see what a function does with the input:

f(x) = x² shows us that function "f" takes "x" and squares it.

Example: with f(x) = x²:

• an input of 4
• becomes an output of 16.

In fact we can write f(4) = 16.

The "x" is Just a Place-Holder!

Don't get too concerned about "x", it is just there to show us where the input goes and what happens to it.

It could be anything!

So this function:

f(x) = 1 - x + x²

Is the same function as:

• f(q) = 1 - q + q²
• h(A) = 1 - A + A²
• w(θ) = 1 - θ + θ²

The variable (x, q, A, etc) is just there so we know where to put the values:

f(2) = 1 - 2 + 2² = 3

Sometimes There is No Function Name

Sometimes a function has no name, and we see something like:

y = x²

But there is still:

• an input (x)
• a relationship (squaring)
• and an output (y)

Relating

At the top we said that a function was like a machine. But a function doesn't really have belts or cogs or any moving parts - and it doesn't actually destroy what we put into it!

A function relates an input to an output.

Saying "f(4) = 16" is like saying 4 is somehow related to 16. Or 4 → 16

Example: this tree grows 20 cm every year, so the height of the tree is related to its age using the function h:

h(age) = age × 20

So, if the age is 10 years, the height is:

h(10) = 10 × 20 = 200 cm

Here are some example values:

age	h(age) = age × 20
0	0
1	20
3.2	64
15	300
...	...

What Types of Things Do Functions Process?

"Numbers" seems an obvious answer, but ...

	... which numbers? For example, the tree-height function h(age) = age×20 makes no sense for an age less than zero.
	... it could also be letters ("A"→"B"), or ID codes ("A6309"→"Pass") or stranger things.

So we need something more powerful, and that is where sets come in:

A set is a collection of things. Here are some examples: Set of even numbers: {..., -4, -2, 0, 2, 4, ...} Set of clothes: {"hat","shirt",...} Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...} Positive multiples of 3 that are less than 10: {3, 6, 9}

Each individual thing in the set (such as "4" or "hat") is called a member, or element.

So, a function takes elements of a set, and gives back elements of a set.

A Function is Special

But a function has special rules:

• It must work for every possible input value
• And it has only one relationship for each input value

This can be said in one definition:

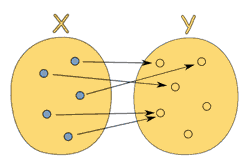Formal Definition of a Function A function relates each element of a set with exactly one element of another set (possibly the same set).

The Two Important Things!

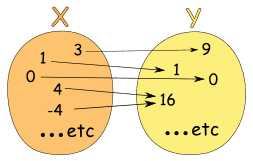
1.	"...each element..." means that every element in X is related to some element in Y. We say that the function covers X (relates every element of it). (But some elements of Y might not be related to at all, which is fine.)

2.	"...exactly one..." means that a function is single valued. It will not give back 2 or more results for the same input. So "f(2) = 7 or 9" is not right!

Note: "One-to-many" is not allowed, but "many-to-one" is allowed:
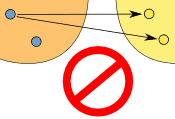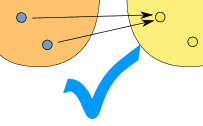(one-to-many)		(many-to-one)
This is NOT OK in a function		But this is OK in a function

When a relationship does not follow those two rules then it is not a function ... it is still arelationship, just not a function.

Example: The relationship x → x²

Could also be written as a table:

X: x	Y: x2
3	9
1	1
0	0
4	16
-4	16
...	...

It is a function, because:

• Every element in X is related to Y
• No element in X has two or more relationships

So it follows the rules.

(Notice how both 4 and -4 relate to 16, which is allowed.)

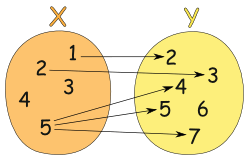
Example: This relationship is not a function:

It is a relationship, but it is not a function, for these reasons:

• Value "3" in X has no relation in Y
• Value "4" in X has no relation in Y
• Value "5" is related to more than one value in Y

(But the fact that "6" in Y has no relationship does not matter)

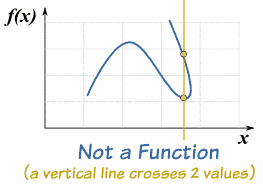Vertical Line Test On a graph, the idea of single valued means that no vertical line ever crosses more than one value. If it crosses more than once it is still a valid curve, but isnot a function.

Some types of functions have stricter rules, to find out more you can read Injective, Surjective and Bijective

Infinitely Many

My examples have just a few values, but functions usually work on sets with infinitely many elements.

Example: y = x³

• The input set "X" is all Real Numbers
• The output set "Y" is also all the Real Numbers

We can't show ALL the values, so here are just a few examples:

X: x	Y: x3
-2	-8
-0.1	-0.001
0	0
1.1	1.331
3	27
and so on...	and so on...

Domain, Codomain and Range

In our examples above

• the set "X" is called the Domain,
• the set "Y" is called the Codomain, and
• the set of elements that get pointed to in Y (the actual values produced by the function) is called the Range.

We have a special page on Domain, Range and Codomain if you want to know more.

So Many Names!

Functions have been used in mathematics for a very long time, and lots of different names and ways of writing functions have come about.

Here are some common terms you should get familiar with:

Example: with z = 2u³:

• "u" could be called the "independent variable"
• "z" could be called the "dependent variable" (it depends on the value of u)

Example: with f(4) = 16:

• "4" could be called the "argument"
• "16" could be called the "value of the function"

Ordered Pairs

And here is another way to think about functions:

Write the input and output of a function as an "ordered pair", such as (4,16).

They are called ordered pairs because the input always comes first, and the output second:

(input, output)

So it looks like this:

( x, f(x) )

Example:

(4,16) means that the function takes in "4" and gives out "16"

Set of Ordered Pairs

A function can then be defined as a set of ordered pairs:

Example: {(2,4), (3,5), (7,3)} is a function that says

"2 is related to 4", "3 is related to 5" and "7 is related 3".

Also, notice that:

• the domain is {2,3,7} (the input values)
• and the range is {4,5,3} (the output values)

But the function has to be single valued, so we also say

"if it contains (a, b) and (a, c), then b must equal c"

Which is just a way of saying that an input of "a" cannot produce two different results.

Example: {(2,4), (2,5), (7,3)} is not a function because {2,4} and {2,5} means that 2 could be related to 4 or 5.

In other words it is not a function because it is not single valued

 

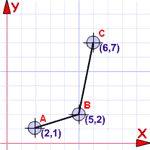A Benefit of Ordered Pairs We can graph them... ... because they are also coordinates! So a set of coordinates is also a function (if they follow the rules above, that is)

A Function Can be in Pieces

We can create functions that behave differently depending on the input value

Example: A function with two pieces:

• when x is less than 0, it gives 5,
• when x is 0 or more it gives x²

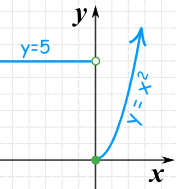Here are some example values: x y -3 5 -1 5 0 0 2 4 4 16 ... ...

Read more at Piecewise Functions.

Explicit vs Implicit

One last topic: the terms "explicit" and "implicit".

"Explicit" is when the function shows us how to go directly from x to y, such as:

y = x³ - 3

When we know x, we can find y

That is the classic y = f(x) style.

"Implicit" is when it is not given directly such as:

x² - 3xy + y³ = 0

When we know x, how do we find y?

It may be hard (or impossible!) to go directly from x to y.

"Implicit" comes from "implied", in other words shown indirectly.

Graphing

• The Function Grapher can only handle explicit functions,
• The Equation Grapher can handle both types (but takes a little longer, and sometimes gets it wrong).

Conclusion

• a function relates inputs to outputs
• a function takes elements from a set (the domain) and relates them to elements in a set (the codomain).
• all the outputs (the actual values related to) are together called the range
• a function is a special type of relation where:
  • every element in the domain is included, and
  • any input produces only one output (not this or that)
• an input and its matching output are together called an ordered pair
• so a function can also be seen as a set of ordered pairs