Geometry
Geometry is all about shapes and their properties.
If you like playing with objects, or like drawing, then geometry is for you!
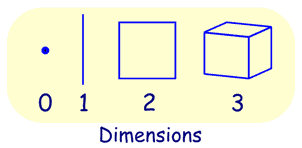
Geometry can be divided into:  | Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper |
 | Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres. |
2D Shapes
Regular Polygons
A polygon is a plane (2D) shape with straight sides.
To be a regular polygon all the sides and angles must be the same:
To be a regular polygon all the sides and angles must be the same:
 Triangle - 3 Sides |  Square - 4 Sides |
 Pentagon - 5 Sides |  Hexagon - 6 sides |
 Heptagon - 7 Sides |  Octagon - 8 Sides |
 Nonagon - 9 Sides |  Decagon - 10 Sides |
Other Common Polygons
 Quadrilateral Any 4 sided 2D shape |  Rectangle - 4 Sides All right angles |
| And many more! | |
Curved Shapes
These 2D shapes have curves, so are not polygons:
 Circle - 1 Side |  Ellipse - 1 Side | |||||||||||||||||||||||||||||||||||||
And many more!Quadrilaterals
Quadrilateral just means "four sides"
(quad means four, lateral means side).
A Quadrilateral has four-sides, it is 2-dimensional (a flat shape), closed (the lines join up), and has straight sides.
Properties
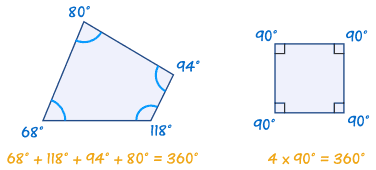
Try drawing a quadrilateral, and measure the angles. They should add to 360°
Types of Quadrilaterals
There are special types of quadrilateral:

Some types are also included in the definition of other types! For example a square, rhombus andrectangle are also parallelograms. See below for more details.
Let us look at each type in turn:
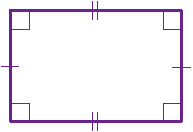
The Rectangle
A rectangle is a four-sided shape where every angle is a right angle (90°).
Also opposite sides are parallel and of equal length.
The Rhombus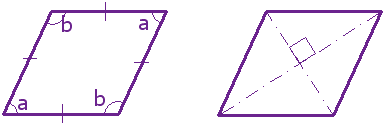
A rhombus is a four-sided shape where all sides have equal length.
Also opposite sides are parallel and opposite angles are equal.
Another interesting thing is that the diagonals (dashed lines in second figure) meet in the middle at a right angle. In other words they "bisect" (cut in half) each other at right angles.
A rhombus is sometimes called a rhomb or a diamond.
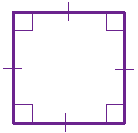
The Square
A square has equal sides and every angle is a right angle (90°)
Also opposite sides are parallel.
A square also fits the definition of a rectangle (all angles are 90°), and a rhombus (all sides are equal length).
The Parallelogram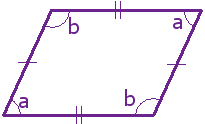
A parallelogram has opposite sides parallel and equal in length. Also opposite angles are equal (angles "a" are the same, and angles "b" are the same).
NOTE: Squares, Rectangles and Rhombuses are all Parallelograms!
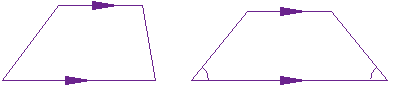
The Trapezoid (UK: Trapezium)
A trapezoid (called a trapezium in the UK) has a pair of opposite sides parallel.
It is called an Isosceles trapezoid if the sides that aren't parallel are equal in length and both angles coming from a parallel side are equal, as shown.
And a trapezium (UK: trapezoid) is a quadrilateral with NO parallel sides:
The Kite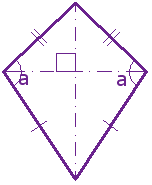
Hey, it looks like a kite. It has two pairs of sides.
Each pair is made up of adjacent sides (they meet) that are equal in length.
The angles are equal where the pairs meet. Diagonals (dashed lines) meet at a right angle, and one of the diagonal bisects (cuts equally in half) the other.
... and that's it for the special quadrilaterals.
Irregular Quadrilaterals
The only regular quadrilateral is a square. So all other quadrilaterals are irregular.
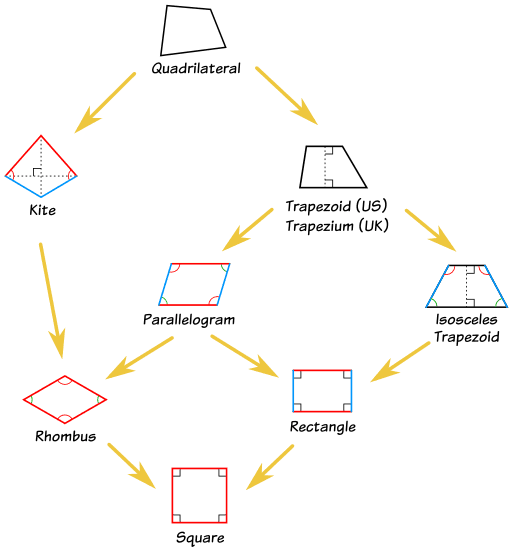
The "Family Tree" Chart
This may seem odd, as in daily life we think of a square as not being a rectangle ... but in mathematics it is.
Using the chart below you can answer such questions as:
 Complex Quadrilaterals
Oh Yes! when two sides cross over, you call it a "Complex" or "Self-Intersecting" quadrilateral like these:
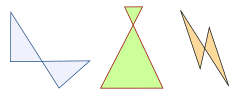
They still have 4 sides, but two sides cross over.
Polygon
A quadrilateral is a polygon. In fact it is a 4-sided polygon, just like a triangle is a 3-sided polygon, a pentagon is a 5-sided polygon, and so on.
Play with Them
Now that you know the different types, you can play with the Interactive Quadrilaterals.
Other Names
A quadrilateral can sometimes be called:
Perimeter | ||||||||||||||||||||||||||||||||||||||
Perimeter is the distance around a two-dimensional shape.
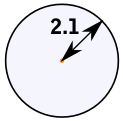
The perimeter of a circle is called the circumference:
Circumference = 2π × radius
|  |
Perimeter Formulas
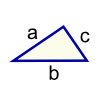 | Triangle Perimeter = a + b + c | |
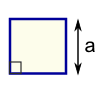 | Square Perimeter = 4 × a a = length of side | |
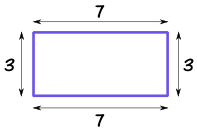
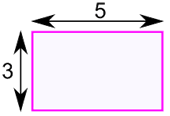
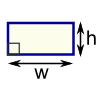 | Rectangle Perimeter = 2 × (w + h) w = width h = height | |
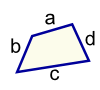 | Quadrilateral Perimeter = a + b + c + d | |
 | Circle Circumference = 2πr r = radius | |
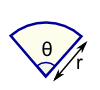 | Sector Perimeter = r(θ+2) r = radius θ = angle in radians | |
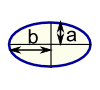 | Ellipse Perimeter = very hard! |
What is Area?
Area is the size of a surface!

It helps to imagine how much paint would cover the shape.
Area of Simple Shapes
There are special formulas for certain shapes:
Learn more at Area of Plane Shapes.
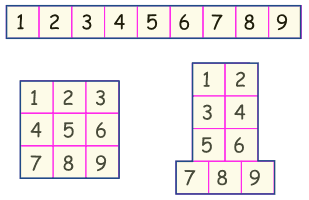
Area by Counting Squares
We can also put the shape on a grid and count the number of squares:
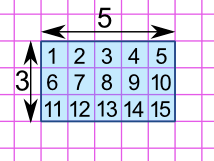
The rectangle has an area of 15
If each square was 1 cm on a side, then the area would be 15 cm2 (15 square cm)
Approximate Area by Counting Squares
Sometimes the squares don't match the shape exactly, but we can get an "approximate" answer.
One way is:
- more than half a square counts as 1
- less than half a square counts as 0
Like this:
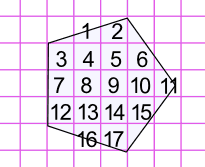
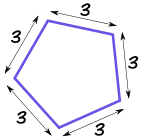
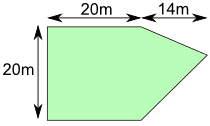
This pentagon has an area of approximately 17
Or we can count one square when the areas seem to add up.
Example: Here the area marked "4" seems equal to about 1 whole square (also for "8"):
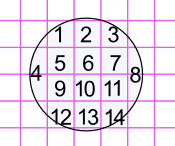
This circle has an area of approximately 14
But using a formula (when possible) is best:
Area of Difficult Shapes
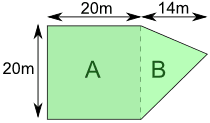
We can sometimes break a shape up into two or more simpler shapes:
Area by Adding Up Triangles
We can also break up a shape into triangles:
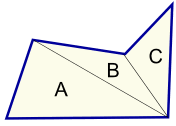
Then measure the base (b) and height (h) of each triangle:
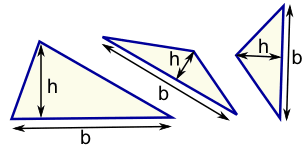
Then calculate each area (using Area = ½b × h) and add them all up.
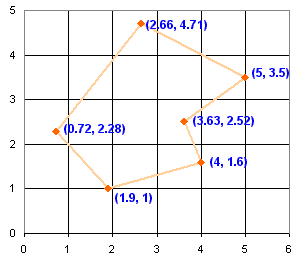
Area by Coordinates
When we know the coordinates of each corner point we can use the Area of Irregular Polygons method.
There is an Area of a Polygon by Drawing Tool that can help too.





No comments:
Post a Comment