Exponents make it easier to write and use many multiplications
Example: 96 is easier to write and read than 9 × 9 × 9 × 9 × 9 × 9
In General
So in general:
an tells you to multiply a by itself,
so there are n of those a's: | | 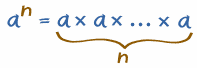 |
Other Way of Writing It
Sometimes people use the ^ symbol (above the 6 on your keyboard), as it is easy to type.
Example: 2^4 is the same as 24
Negative Exponents
Negative? What could be the opposite of multiplying?
Dividing!
A negative exponent means how many times to divide one by the number.
Example: 8-1 = 1 ÷ 8 = 0.125
You can have many divides:
Example: 5-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0.008
But that can be done an easier way:
5-3 could also be calculated like:
1 ÷ (5 × 5 × 5) = 1/53 = 1/125 = 0.008
In General
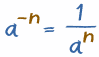 |
That last example showed an easier way to handle negative exponents:
- Calculate the positive exponent (an)
- Then take the Reciprocal (i.e. 1/an)
|
More Examples:
| Negative Exponent | | Reciprocal of Positive Exponent | | Answer |
|---|
| 4-2 | = | 1 / 42 | = | 1/16 = 0.0625 |
| 10-3 | = | 1 / 103 | = | 1/1,000 = 0.001 |
| (-2)-3 | = | 1 / (-2)3 | = | 1/(-8) = -0.125 |
What if the Exponent is 1, or 0?
| 1 | | If the exponent is 1, then you just have the number itself (example 91 = 9) |
| | | |
| 0 | | If the exponent is 0, then you get 1 (example 90 = 1) |
| | | |
| | | But what about 00 ? It could be either 1 or 0, and so people say it is "indeterminate". |
It All Makes Sense
My favorite method is to start with "1" and then multiply or divide as many times as the exponent says, then you will get the right answer, for example:
| Example: Powers of 5 |
|---|
| | .. etc.. | |  |
| 52 | 1 × 5 × 5 | 25 |
| 51 | 1 × 5 | 5 |
| 50 | 1 | 1 |
| 5-1 | 1 ÷ 5 | 0.2 |
| 5-2 | 1 ÷ 5 ÷ 5 | 0.04 |
| | .. etc.. | |
If you look at that table, you will see that positive, zero or negative exponents are really part of the same (fairly simple) pattern.
Be Careful About Grouping
To avoid confusion, use parentheses () in cases like this:
| With () : | (-2)2 = (-2) × (-2) = 4 |
| Without () : | -22 = -(22) = - (2 × 2) = -4 |
| With () : | (ab)2 = ab × ab |
| Without () : | ab2 = a × (b)2 = a × b × b |
Reciprocal In Algebra
Turn it upside down!
Reciprocal of a Number
To get the reciprocal of a number, just divide 1 by the number.
|  |
Examples:
| Number | Reciprocal | As a Decimal |
|---|
| 2 | 1/2 | = 0.5 |
| 8 | 1/8 | = 0.125 |
| 1,000 | 1/1,000 | = 0.001 |
Reciprocal of a Variable
If you are given a variable "x", its reciprocal is "1/x".
Likewise, if you are given something more complicated like "x/y" then the reciprocal is just "y/x". In other words turn it upside down.
|  |
Example: What is the Reciprocal of x/(x-1) ?
Answer: take x/(x-1) and flip it upside down: (x-1)/x
Flipping a Flip
If you take the reciprocal of a reciprocal you end up back where you started!
Example:
The reciprocal of ax/y is y/ax
The reciprocal of y/ax is ax/y (back again)
Example: What is:
Answer: w
Notation
The reciprocal of "x" is shown as:
Squares and Square Roots
First learn about Squares, then Square Roots are easy.
How to Square A Number
To square a number, just multiply it by itself ...
Example: What is 3 squared?
| 3 Squared | = | 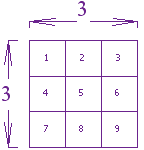 | = 3 × 3 = 9 |
"Squared" is often written as a little 2 like this:
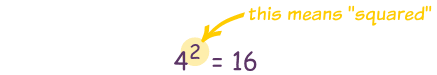
This says
"4 Squared equals 16"
(the little 2 says the number appears twice in multiplying)
Squares From 12 to 62
| 1 Squared | = | 12 | = | 1 × 1 | = | 1 |
| 2 Squared | = | 22 | = | 2 × 2 | = | 4 |
| 3 Squared | = | 32 | = | 3 × 3 | = | 9 |
| 4 Squared | = | 42 | = | 4 × 4 | = | 16 |
| 5 Squared | = | 52 | = | 5 × 5 | = | 25 |
| 6 Squared | = | 62 | = | 6 × 6 | = | 36 |
The squares are also
on the Multiplication Table: | | 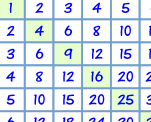 |
Negative Numbers
We can also square negative numbers.
Example: What happens when we square (−5) ?
Answer:
(−5) × (−5) = 25
(because a negative times a negative gives a positive)
That was interesting!
When we square a negative number we get a positive result.
Just the same as squaring a positive number:
(For more detail read Squares and Square Roots in Algebra)
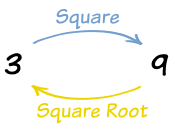
Square Roots
A square root goes the other way:
3 squared is 9, so a square root of 9 is 3
A square root of a number is ...
... a value that can be multiplied by itself to give the original number.
A square root of 9 is ...
... 3, because when 3 is multiplied by itself we get 9.
It is like asking:
What can we multiply by itself to get this?
 |
To help you remember think of the root of a tree:
"I know the tree, but what is the root that made it?"
In this case the tree is "9", and the root is "3".
|
Here are some more squares and square roots:
 |
4
| |
16
|
5
| |
25
|
6
| |
36
|
Decimal Numbers
It also works for decimal numbers.
- What is the square root of 8?
- What is the square root of 9?
- What is the square root of 10?
- What is 1 squared?
- What is 1.1 squared?
- What is 2.6 squared?
Negatives
We found out before that we can square negative numbers:
Example: (−3) squared
(−3) × (−3) = 9
And of course 3 × 3 = 9 also.
So the square root of 9 could be −3 or +3
Example: What are the square roots of 25?
(−5) × (−5) = 25
5 × 5 = 25
So the square roots of 25 are −5 and +5
The Square Root Symbol
 | | This is the special symbol that means "square root", it is sort of like a tick,
and actually started hundreds of years ago as a dot with a flick upwards.
It is called the radical, and always makes mathematics look important! |
We use it like this:
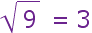
and we say
"square root of 9 equals 3"
Example: What is √25?
Well, we just happen to know that 25 = 5 × 5, so when we multiply 5 by itself (5 × 5) we will get 25.
So the answer is:
√25 = 5
But wait a minute! Can't the square root also be −5? Because (−5) × (−5) = 25 too.
- Well the square root of 25 could be −5 or +5.
- But when we use the radical symbol √ we only give the positive (or zero) result.
Example: What is √36 ?
Answer: 6 × 6 = 36, so √36 = 6
Perfect Squares
The Perfect Squares (also called "Square Numbers") are the squares of the whole numbers:
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | etc |
| Perfect Squares: | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | ... |
Try to remember at least the first 10 of those.
Calculating Square Roots
It is easy to work out the square root of a perfect square, but it is really hard to work out other square roots.
Example: what is √10?
Well, 3 × 3 = 9 and 4 × 4 = 16, so we can guess the answer is between 3 and 4.
- Let's try 3.5: 3.5 × 3.5 = 12.25
- Let's try 3.2: 3.2 × 3.2 = 10.24
- Let's try 3.1: 3.1 × 3.1 = 9.61
- ...
Getting closer to 10, but it will take a long time to get a good answer!
 |
At this point, I get out my calculator and it says:
3.1622776601683793319988935444327
But the digits just go on and on, without any pattern.
So even the calculator's answer is only an approximation !
|
Note: numbers like that are called Irrational Numbers, if you want to know more.
The Easiest Way to Calculate a Square Root
 | | Use your calculator's square root button! | |  |
And also use your common sense to make sure you have the right answer.
A Fun Way to Calculate a Square Root
There is a fun method for calculating a square root that gets more and more accurate each time around:
| | a) start with a guess (let's guess 4 is the square root of 10) |
 | b) divide by the guess (10/4 = 2.5)
c) add that to the guess (4 + 2.5 = 6.5)
d) then divide that result by 2, in other words halve it. (6.5/2 = 3.25)
e) now, set that as the new guess, and start at b) again |
- Our first attempt got us from 4 to 3.25
- Going again (b to e) gets us: 3.163
- Going again (b to e) gets us: 3.1623
And so, after 3 times around the answer is 3.1623, which is pretty good, because:
3.1623 x 3.1623 = 10.00014
Now ... why don't you try calculating the square root of 2 this way?
How to Guess
What if we have to guess the square root for a difficult number such as "82,163" ... ?
In that case we could think "82,163" has 5 digits, so the square root might have 3 digits (100x100=10,000), and the square root of 8 (the first digit) is about 3 (3x3=9), so 300 is a good start.
Square Root Day
The 4th of April 2016 is a Square Root Day, because the date looks like 4/4/16
The next after that is the 5th of May 2025 (5/5/25)
Factoring in Algebra
Factors
Numbers have factors:
And expressions (like x2+4x+3) also have factors:
Factoring
Factoring (called "Factorising" in the UK) is the process of finding the factors:
Factoring: Finding what to multiply together to get an expression.
It is like "splitting" an expression into a multiplication of simpler expressions.
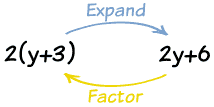
Example: factor 2y+6
Both 2y and 6 have a common factor of 2:
So you can factor the whole expression into:
2y+6 = 2(y+3)
So 2y+6 has been "factored into" 2 and y+3
Factoring is also the opposite of Expanding:
Common Factor
In the previous example we saw that 2y and 6 had a common factor of 2
But to do the job properly make sure you have the highest common factor, including any variables
Example: factor 3y2+12y
Firstly, 3 and 12 have a common factor of 3.
So you could have:
3y2+12y = 3(y2+4y)
But we can do better!
3y2 and 12y also share the variable y.
Together that makes 3y:
- 3y2 is 3y × y
- 12y is 3y × 4
So you can factor the whole expression into:
3y2+12y = 3y(y+4)
Check: 3y(y+4) = 3y × y + 3y × 4 = 3y2+12y
More Complicated Factoring
Factoring Can Be Hard !
The examples have been simple so far, but factoring can be very tricky.
Because you have to figure what got multiplied to produce the expression you are given!
 | It can be like trying to find out what ingredients went into a cake to make it so delicious. It is sometimes not obvious at all! |
Experience Helps
But the more experience you get, the easier it becomes.
Example: Factor 4x2 - 9
Hmmm... I can't see any common factors.
But if you know your Special Binomial Products you might see it as the "difference of squares":
Because 4x2 is (2x)2, and 9 is (3)2,
so we have:
4x2 - 9 = (2x)2 - (3)2
And that can be produced by the difference of squares formula:
(a+b)(a-b) = a2 - b2
Where a is 2x, and b is 3.
So let us try doing that:
(2x+3)(2x-3) = (2x)2 - (3)2 = 4x2 - 9
Yes!
So the factors of 4x2 - 9 are (2x+3) and (2x-3):
Answer: 4x2 - 9 = (2x+3)(2x-3)
How can you learn to do that? By getting lots of practice, and knowing "Identities"!
Remember these Identities
Here is a list of common "Identities" (including the "difference of squares" used above).
It is worth remembering these, as they can make factoring easier.
 |
| a2 - b2 | = | (a+b)(a-b) |
| a2 + 2ab + b2 | = | (a+b)(a+b) |
| a2 - 2ab + b2 | = | (a-b)(a-b) |
| a3 + b3 | = | (a+b)(a2-ab+b2) |
| a3 - b3 | = | (a-b)(a2+ab+b2) |
| a3+3a2b+3ab2+b3 | = | (a+b)3 |
| a3-3a2b+3ab2-b3 | = | (a-b)3 |
There are many more like those, but those are the simplest ones.
Advice
The factored form is usually best.
When trying to factor, follow these steps:
- "Factor out" any common terms
- See if it fits any of the identities, plus any more you may know
- Keep going till you can't factor any more
You can also use computers! There are Computer Algebra Systems (called "CAS") such as Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce and many more that are good at factoring.
More Examples
I said that experience helps, so here are more examples to help you on the way:
Example: w4 - 16
An exponent of 4? Maybe we could try an exponent of 2:
w4 - 16 = (w2)2 - 42
Yes, it is the difference of squares
w4 - 16 = (w2 + 4)(w2 - 4)
And "(w2 - 4)" is another difference of squares
w4 - 16 = (w2 + 4)(w + 2)(w - 2)
That is as far as I can go (unless I use imaginary numbers)
Example: 3u4 - 24uv3
Remove common factor "3u":
3u4 - 24uv3 = 3u(u3 - 8v3)
Then a difference of cubes:
3u4 - 24uv3 = 3u(u3 - (2v)3)
= 3u(u-2v)(u2+2uv+4v2)
That is as far as I can go.
Example: z3 - z2 - 9z + 9
Try factoring the first two and second two separately:
z2(z-1) - 9(z-1)
Wow, (z-1) is on both, so let us use that:
(z2-9)(z-1)
And z2-9 is a difference of squares
(z-3)(z+3)(z-1)
That is as far as I can go.
Introduction to Logarithms
In its simplest form, a logarithm answers the question:
How many of one number do we multiply to get another number?
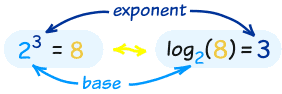
Example: How many 2s do we multiply to get 8?
Answer: 2 × 2 × 2 = 8, so we needed to multiply 3 of the 2s to get 8
So the logarithm is 3
How to Write it
We write "the number of 2s we need to multiply to get 8 is 3" as:
log2(8) = 3
So these two things are the same:
The number we are multiplying is called the "base", so we can say:
- "the logarithm of 8 with base 2 is 3"
- or "log base 2 of 8 is 3"
- or "the base-2 log of 8 is 3"
Notice we are dealing with three numbers:
- the base: the number we are multiplying (a "2" in the example above)
- how many times to use it in a multiplication (3 times, which is the logarithm)
- The number we want to get (an "8")
More Examples
Example: What is log5(625) ... ?
We are asking "how many 5s need to be multiplied together to get 625?"
5 × 5 × 5 × 5 = 625, so we need 4 of the 5s
Answer: log5(625) = 4
Example: What is log2(64) ... ?
We are asking "how many 2s need to be multiplied together to get 64?"
2 × 2 × 2 × 2 × 2 × 2 = 64, so we need 6 of the 2s
Answer: log2(64) = 6
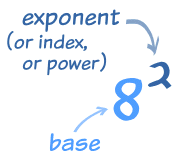
Exponents
Exponents and Logarithms are related, let's find out how ...
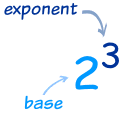 |
The exponent says how many times to use the number in a multiplication.
In this example: 23 = 2 × 2 × 2 = 8
(2 is used 3 times in a multiplication to get 8)
|
So a logarithm answers a question like this:
In this way:
The logarithm tells us what the exponent is!
In that example the "base" is 2 and the "exponent" is 3:
So the logarithm answers the question:
What exponent do we need
(for one number to become another number) ?
The general case is:
Example: What is log10(100) ... ?
102 = 100
So an exponent of 2 is needed to make 10 into 100, and:
log10(100) = 2
Example: What is log3(81) ... ?
34 = 81
So an exponent of 4 is needed to make 3 into 81, and:
log3(81) = 4
Common Logarithms: Base 10
Sometimes a logarithm is written without a base, like this:
log(100)
This usually means that the base is really 10.
It is called a "common logarithm". Engineers love to use it.
On a calculator it is the "log" button.
It is how many times we need to use 10 in a multiplication, to get our desired number.
Example: log(1000) = log10(1000) = 3
Natural Logarithms: Base "e"
Another base that is often used is e (Euler's Number) which is about 2.71828.
This is called a "natural logarithm". Mathematicians use this one a lot.
On a calculator it is the "ln" button.
It is how many times we need to use "e" in a multiplication, to get our desired number.
Example: ln(7.389) = loge(7.389) ≈ 2
Because 2.718282 ≈ 7.389
But Sometimes There Is Confusion ... !
Mathematicians use "log" (instead of "ln") to mean the natural logarithm. This can lead to confusion:
| Example | Engineer Thinks | Mathematician Thinks | |
|---|
| log(50) | log10(50) | loge(50) | confusion |
| ln(50) | loge(50) | loge(50) | no confusion |
| log10(50) | log10(50) | log10(50) | no confusion |
So, be careful when you read "log" that you know what base they mean!
Logarithms Can Have Decimals
All of our examples have used whole number logarithms (like 2 or 3), but logarithms can have decimal values like 2.5, or 6.081, etc.
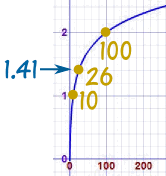
Example: what is log10(26) ... ?
 |
Get your calculator, type in 26 and press log
Answer is: 1.41497...
|
The logarithm is saying that 101.41497... = 26
(10 with an exponent of 1.41497... equals 26)
This is what it looks like on a graph:
See how nice and smooth the line is.
| |  |
Read Logarithms Can Have Decimals to find out more.
Negative Logarithms
| − | Negative? But logarithms deal with multiplying.
What could be the opposite of multiplying? Dividing! |
A negative logarithm means how many times to divide by the number.
We could have just one divide:
Example: What is log8(0.125) ... ?
Well, 1 ÷ 8 = 0.125,
So log8(0.125) = −1
Or many divides:
Example: What is log5(0.008) ... ?
1 ÷ 5 ÷ 5 ÷ 5 = 5−3,
So log5(0.008) = −3
It All Makes Sense
Multiplying and Dividing are all part of the same simple pattern.
Let us look at some Base-10 logarithms as an example:
| | Number | How Many 10s | Base-10 Logarithm |
|---|
 | .. etc.. | | | |
| 1000 | 1 × 10 × 10 × 10 | log10(1000) | = 3 |
| 100 | 1 × 10 × 10 | log10(100) | = 2 |
| 10 | 1 × 10 | log10(10) | = 1 |
| 1 | 1 | log10(1) | = 0 |
| 0.1 | 1 ÷ 10 | log10(0.1) | = −1 |
| 0.01 | 1 ÷ 10 ÷ 10 | log10(0.01) | = −2 |
| 0.001 | 1 ÷ 10 ÷ 10 ÷ 10 | log10(0.001) | = −3 |
| .. etc.. | | | |
Looking at that table, see how positive, zero or negative logarithms are really part of the same (fairly simple) pattern.
The Word
"Logarithm" is a word made up by Scottish mathematician John Napier (1550-1617), from the Greek word logos meaning "proportion, ratio or word" andarithmos meaning "number", ... which together makes "ratio-number" !







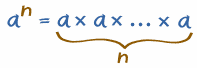
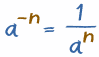






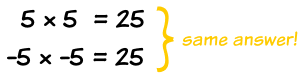




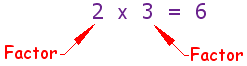
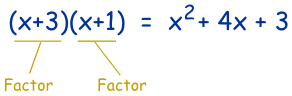
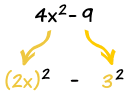



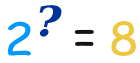
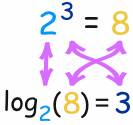
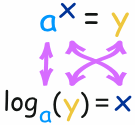




No comments:
Post a Comment