The Derivative tells us the slope of a function at any point.
The derivatives of many functions are well known. Here are some useful rules to help you work out the derivatives of more complicated functions (with examples below). Note: the little mark ’means "Derivative of".
| Common Functions | Function | Derivative |
|---|
| Constant | c | 0 |
| | x | 1 |
| Square | x2 | 2x |
| Square Root | √x | (½)x-½ |
| Exponential | ex | ex |
| | ax | ax(ln a) |
| Logarithms | ln(x) | 1/x |
| | loga(x) | 1 / (x ln(a)) |
| Trigonometry (x is in radians) | sin(x) | cos(x) |
| | cos(x) | −sin(x) |
| | tan(x) | sec2(x) |
| | sin-1(x) | 1/√(1−x2) |
| | cos-1(x) | −1/√(1−x2) |
| | tan-1(x) | 1/(1+x2) |
| | | |
| Rules | Function | Derivative |
|---|
| Multiplication by constant | cf | cf’ |
| Power Rule | xn | nxn−1 |
| Sum Rule | f + g | f’ + g’ |
| Difference Rule | f - g | f’ − g’ |
| Product Rule | fg | f g’ + f’ g |
| Quotient Rule | f/g | (f’ g − g’ f )/g2 |
| Reciprocal Rule | 1/f | −f’/f2 |
Chain Rule
(as "Composition of Functions") | f º g | (f’ º g) × g’ |
| Chain Rule (in a different form) | f(g(x)) | f’(g(x))g’(x) |
"The derivative of" is also written
Examples
Example: what is the derivative of sin(x) ?
From the table above it is listed as being cos(x)
It can be written as:
sin(x) = cos(x)
Or:
sin(x)’ = cos(x)
Power Rule
Example: What is x3 ?
The question is asking "what is the derivative of x3?"
We can use the Power Rule, where n=3:
x
n = nx
n−1
x
3 = 3x
3−1 =
3x2
Example: What is (1/x) ?
1/x is also x-1
We can use the Power Rule, where n = −1:
x
n = nx
n−1
x
−1 = −1x
−1−1 =
−x−2
Multiplication by constant
Example: What is 5x3 ?
the derivative of cf = cf’
the derivative of 5f = 5f’
We know (from the Power Rule):
x
3 = 3x
3−1 = 3x
2
So:
5x
3 = 5
x
3 = 5 × 3x
2 =
15x2
Sum Rule
Example: What is the derivative of x2+x3 ?
The Sum Rule says:
the derivative of f + g = f’ + g’
So we can work out each derivative separately and then add them.
Using the Power Rule:
- x2 = 2x
- x3 = 3x2
And so:
the derivative of x2 + x3 = 2x + 3x2
Difference Rule
It doesn't have to be x, we can differentiate with respect to, for example, v:
Example: What is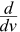 
(v3−v4) ?
The Difference Rule says
the derivative of f − g = f’ − g’
So we can work out each derivative separately and then subtract them.
Using the Power Rule:
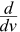- v3 = 3v2
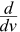- v4 = 4v3
And so:
the derivative of v3 − v4 = 3v2 − 4v3
Sum, Difference, Constant Multiplication And Power Rules
Example: What is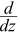 
(5z2 + z3 − 7z4) ?
Using the Power Rule:
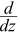- z2 = 2z
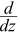- z3 = 3z2
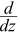- z4 = 4z3
And so:
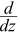
(5z
2 + z
3 − 7z
4) = 5 × 2z + 3z
2 − 7 × 4z
3 =
10z + 3z2 − 28z3
Product Rule
Example: What is the derivative of cos(x)sin(x) ?
The Product Rule says:
the derivative of fg = f g’ + f’ g
In our case:
We know (from the table above):
- cos(x) = −sin(x)
- sin(x) = cos(x)
So:
the derivative of cos(x)sin(x) = cos(x)cos(x) − sin(x)sin(x)
= cos2(x) − sin2(x)
Reciprocal Rule
Example: What is (1/x) ?
The Reciprocal Rule says:
the derivative of 1/f = −f’/f2
With f(x)= x, we know that f’(x) = 1
So:
the derivative of 1/x = −1/x2
Which is the same result we got above using the Power Rule.
Chain Rule
Example: What is sin(x2) ?
sin(x2) is made up of sin() and x2:
The Chain Rule says:
the derivative of f(g(x)) = f'(g(x))g'(x)
The individual derivatives are:
- f'(g) = cos(g)
- g'(x) = 2x
So:
sin(x2) = cos(g(x)) × 2x
= 2x cos(x2)
Example: What is (1/sin(x)) ?
1/sin(x) is made up of 1/g and sin():
The Chain Rule says:
the derivative of f(g(x)) = f’(g(x))g’(x)
The individual derivatives are:
- f'(g) = −1/(g2)
- g'(x) = cos(x)
So:
(1/sin(x))’ = −1/(g(x))2 × cos(x)
= −cos(x)/sin2(x)
Example: What is (5x−2)3 ?
The Chain Rule says:
the derivative of f(g(x)) = f’(g(x))g’(x)
(5x-2)3 is made up of g3 and 5x-2:
The individual derivatives are:
- f'(g) = 3g2 (by the Power Rule)
- g'(x) = 5
So:
(5x−2)3 = 3g(x)2 × 5 = 15(5x−2)2
No comments:
Post a Comment